こんにちは、blueです。
前回は1章から4章の統計問題を勉強しました。
今回は5章から10章のExcelを使った統計問題について理解します。ここまでが実践問題のメインになります。
この記事では、統計用語の意味を明快に解説し、資格取得までに導く情報をお届けします。統計学への第一歩を踏み出すあなたにとって、貴重な参考となることでしょう。一緒に学んでいきましょう!
エクセルを使った統計において仮説検定を勉強したい方は以下がお勧めです。エクセルの「データ分析」アドインを使用するので難しい計算式などはでてきませんし、資格取得も可能です。平易な言葉が使われているので数学が苦手な人でも理解しやすい書籍です。
エクセルを使った統計について一から勉強したい方は以下がお勧めです。平均や中央値など統計で用いる基本的な項目を平易な言葉でわかりやすく説明してくれています。仮説検定を勉強する前に読んでおくとよい書籍です。
Excelを使った統計について一通り勉強したい方は以下がお勧めです。やや数学的な計算が入った説明がありますが最低限の数式で統計を使いこなせるようにしてくださっています。
5章 カイ二乗検定
カイ二乗検定での計算方法
カイ二乗検定は質的変数と質的変数の間の関係を調べる為に用います。
1.ピボットテーブルで行に原因系、列に結果系のクロス集計表を作る
ピボットテーブルについては以下の記事を参考ください。
2.比較用の「差がない」集計表(期待度数による集計表)を作成する(以下図)
1.原因系の集計を出す
2.原因系の構成比率を出す
3.元のピボットテーブルに対して構成比率をかけて期待度数による集計表を作る
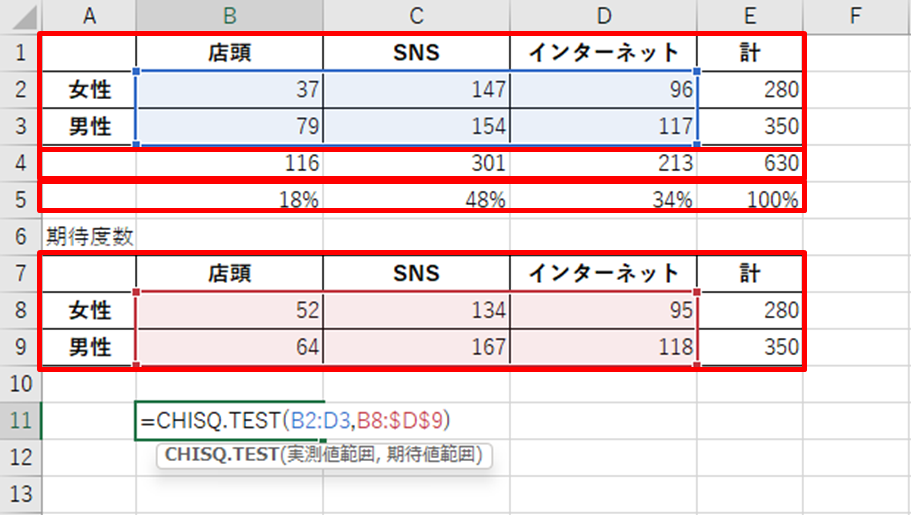
3.カイ二乗検定であるCHISQ.TEST(観測度数の値, 期待度数の値)で有意確率を出す。
結果としてカイ二乗検定による有意確率pが算出されます。
この方法により質的変数と質的変数の間に因果関係=関連があるかを確認することができます。
6章 t検定
F検定での計算方法
F検定は2つのデータのばらつきが同じかどうかを調べる為に用います。
1.原因系変数を並び替える
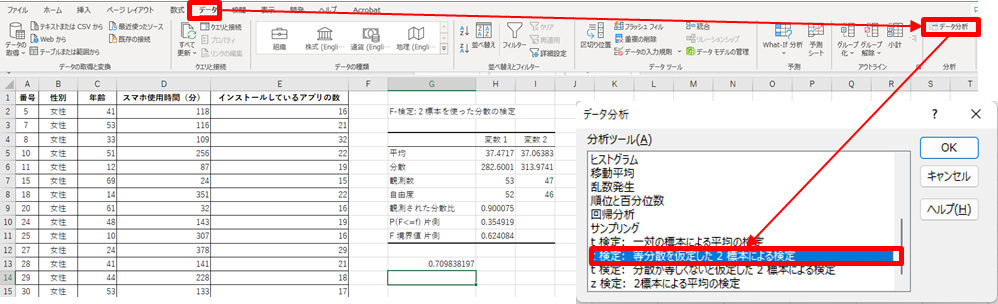
2.[データ]ー[データ分析]-[F検定]を選択する
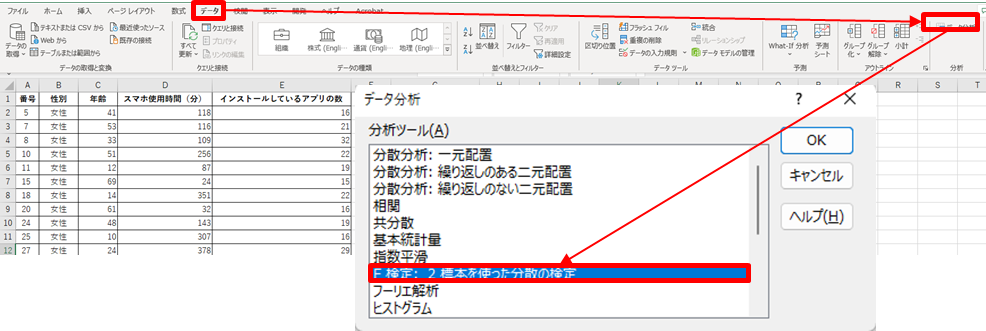
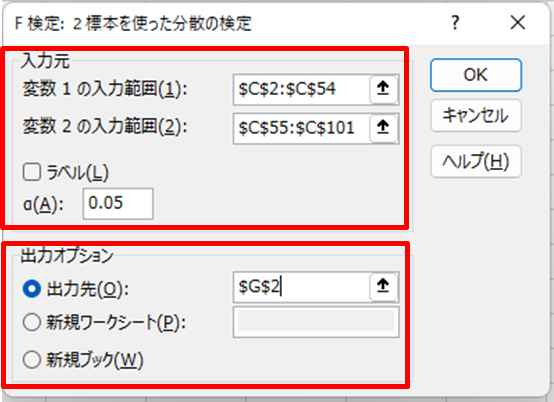
3.入力元を設定する(以下図)
1.(原因系)変数1の「入力範囲」を入力する
2.(原因系)変数1の「入力範囲」を入力する
3.(先頭行がラベルの場合)チェックを入れる
4.出力オプションを設定する
1.「出力先」を設定する(同じワークシートも可)
5.[P(F<=f)片側]を見る。両側の場合は2倍する
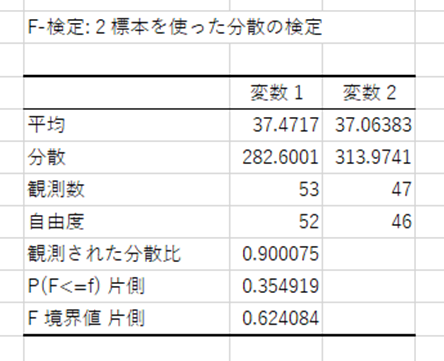
この方法により2つのデータのばらつきが同等かを確認することができます。
t検定での計算方法
t検定は2つのデータの平均値に差があるかどうかを調べる為に用います。
1.F検定のp値≧0.05・・・差はたまたま=等分散
F検定のp値≦0.05・・・差はある=分散は等しくないとする
2.[データ]ー[データ分析]-[t検定:●●(以下表)]を選択する
| 質的変数 | 検定 |
| 質的変数が2択 | (等分散) t検定:等分散を想定した2標本による検定 を用いる |
| 質的変数が2択 | (等分散でない) t検定:分散が等しくないと仮定した2標本による検定 を用いる |
| 質的変数が3択以上 | 一元配置分散分析 を用いる |
| 質的変数が一対の関係 | t検定:一対の標本による平均の検定 を用いる 例:同じ回答者 |
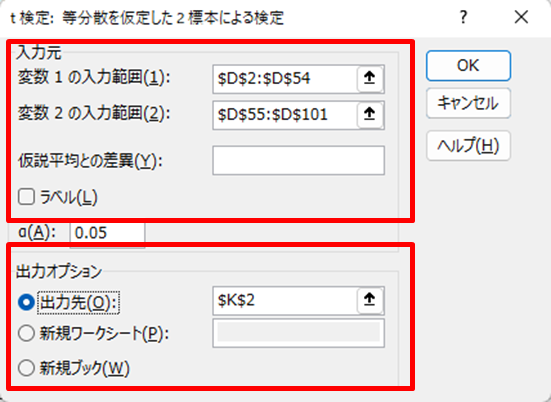
3.入力元を設定する(以下図)
1.(原因系)変数1の「入力範囲」を入力する
2.(原因系)変数1の「入力範囲」を入力する
3.(先頭行がラベルの場合)チェックを入れる
4.出力オプションを設定する
1.「出力先」を設定する(同じワークシートも可)
5.[P-値]を見る
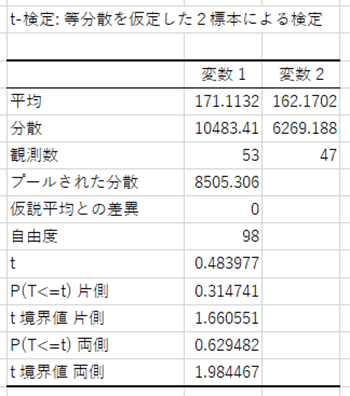
この方法により2つのデータの平均値に差があるかを確認することができます。
一元配置分析での計算方法
一元配置分析は3つ以上のデータの平均値に差があるかどうかを調べる為に用います。
1.事前に比較するグループの値を行か列の方向に並べておく
2.[データ]ー[データ分析]-[分散分析:一元配置]を選択する
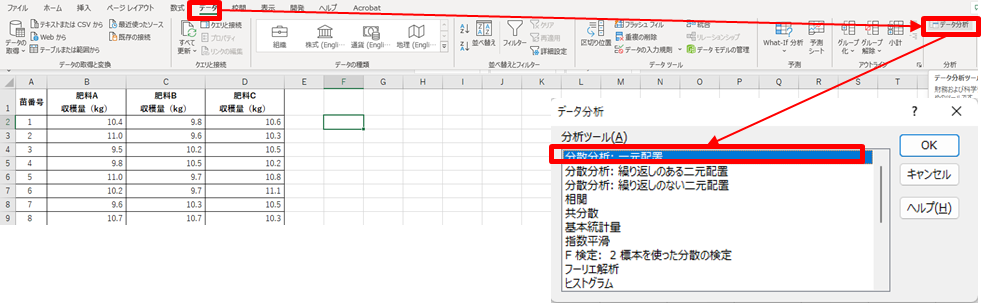
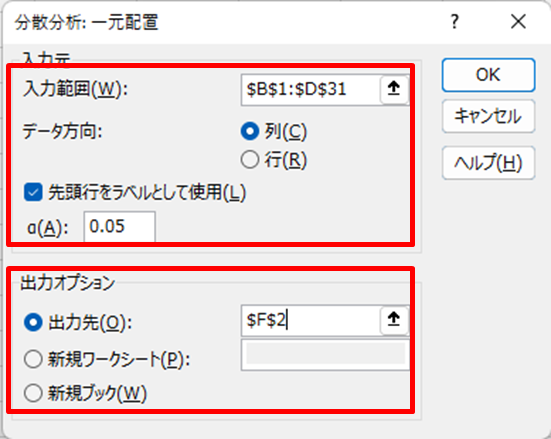
3.入力元を設定する(以下図)
1.グループの「入力範囲」を入力する
2.適したデータ方向にチェックを入れる
3.(先頭行がラベルの場合)チェックを入れる
4.出力オプションを設定する
1.「出力先」を設定する(同じワークシートも可)
5.[P-値]を見る
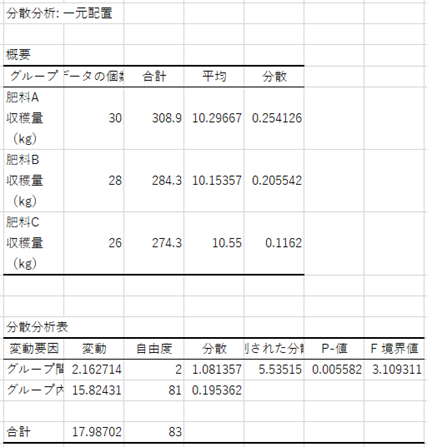
この方法により3つ以上のデータの平均値に差があるかを確認することができます。
7章 相関分析と回帰分析
回帰分析での計算方法
回帰分析は量的変数間の因果関係を調べる為に用います。
1.[データ]ー[データ分析]-[回帰分析]を選択する
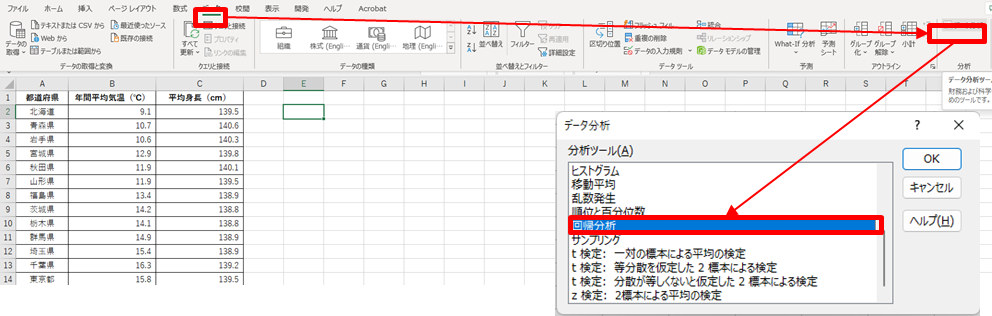
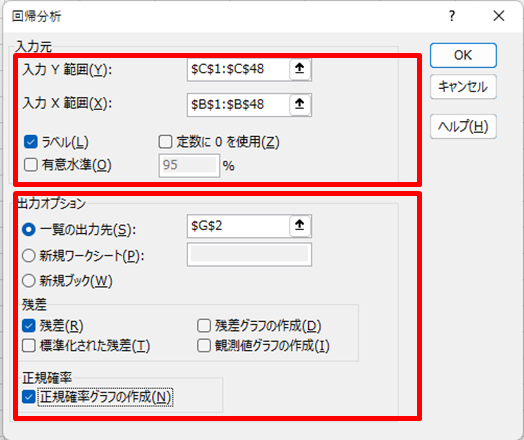
2.入力元を設定する(以下図)
1.「入力X範囲」(原因系)を入力する
2.「入力Y範囲」(結果系)を入力する
3.(先頭行がラベルの場合)チェックを入れる
3.出力オプションを設定する
1.「出力先」を設定する(同じワークシートも可)
2.必要であれば[残差]、[正規確率グラフ]にチェックを入れる
4.[重決定R2]、[係数]、[P-値]を見る
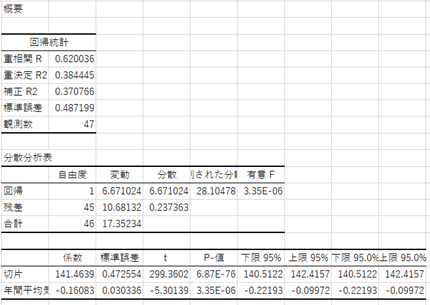
この方法により変数間の因果関係を調べることができます。
8章 ダミー変数
ダミー変数(結果系変数)での計算方法
結果系のダミー変数は原因系変数が量的変数、結果系変数が質的変数の際に用います。
1.着目する選択肢を1にし、If文でダミー変数を作成する(以下図)
1.列名は「元の列名+D」とする
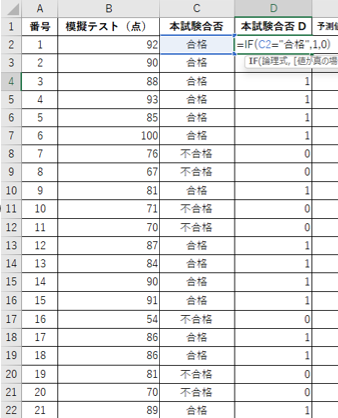
2.量的変数とダミー変数で回帰分析を行う
1.予測値用に残差にチェックを入れる
3.予測値をもとのデータ列の右に追加する
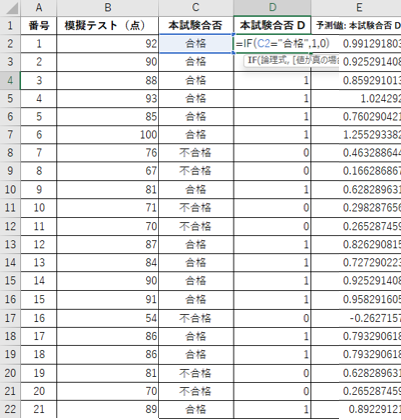
4.If文で予測値を2択の変数に再変換する
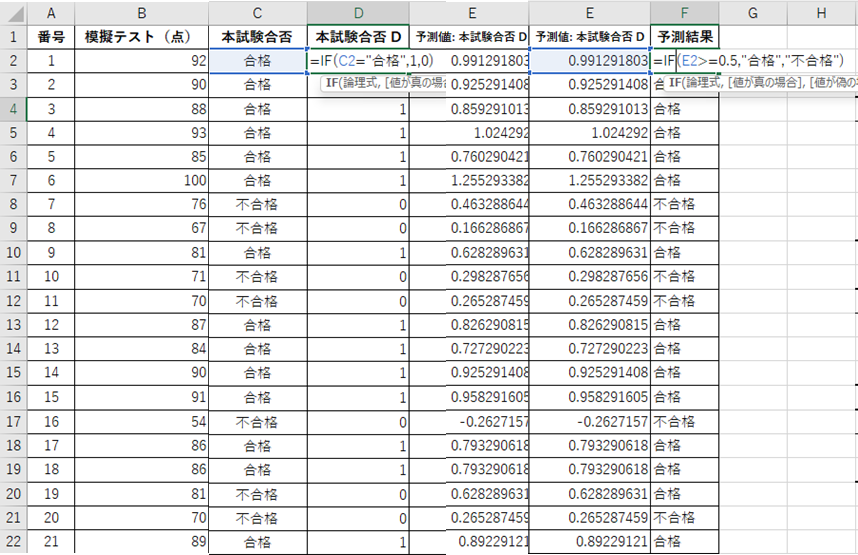
5.ピボットテーブルで正答率を確認する。赤枠が予測が当たっている件数
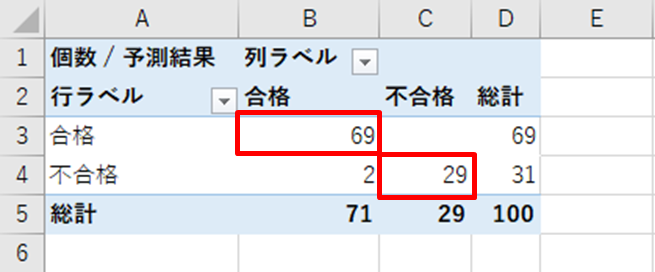
この方法により結果系変数が質的変数の場合でも回帰分析を行うことができます。
9章 重回帰分析
重回帰分析での計算方法
重回帰分析は2つ以上の変数が別の変数に影響を与えるかを調べる為に用います。
1.[データ]ー[データ分析]-[回帰分析]を選択する
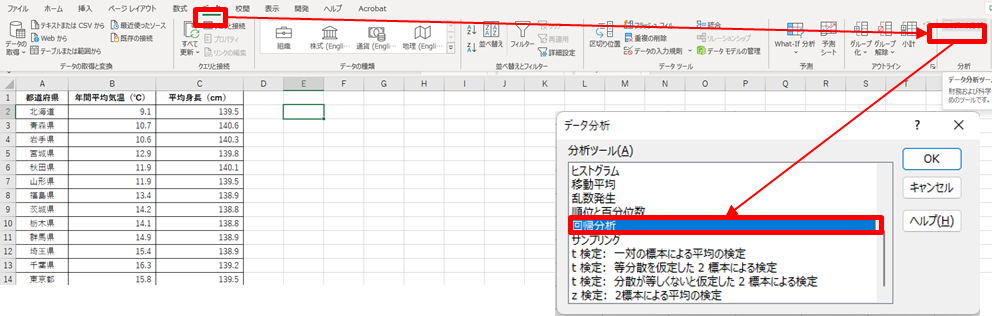
2.入力元を設定する(以下図)
1.「入力X範囲」(原因系)を入力する
(連続する列にすること)
2.「入力Y範囲」(結果系)を入力する
3.(先頭行がラベルの場合)チェックを入れる
3.出力オプションを設定する
1.「出力先」を設定する(同じワークシートも可)
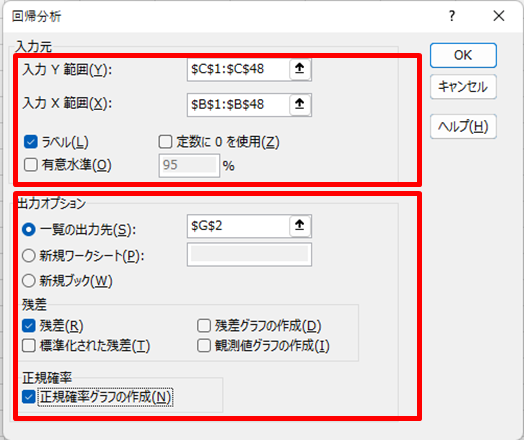
4.[重決定R2]、 [補正R2]、[係数]、[P-値]を見る
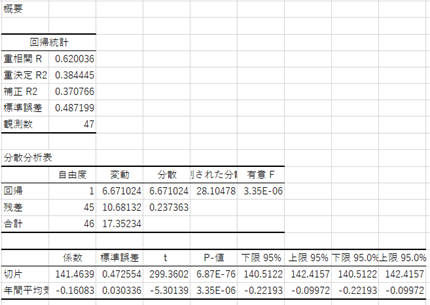
この方法により2つ以上の2つ以上の変数が別の変数に影響を与えるかを調べることができます。
10章 ダミー変数の応用
ダミー変数(原因系変数)の計算方法
結果系のダミー変数は原因系変数が3つ以上の選択肢、結果系変数が量的変数の際に用います。
1.原因系の質的変数をIf文を使ってダミー変数に変換する
1.列名は「選択肢+D」とする
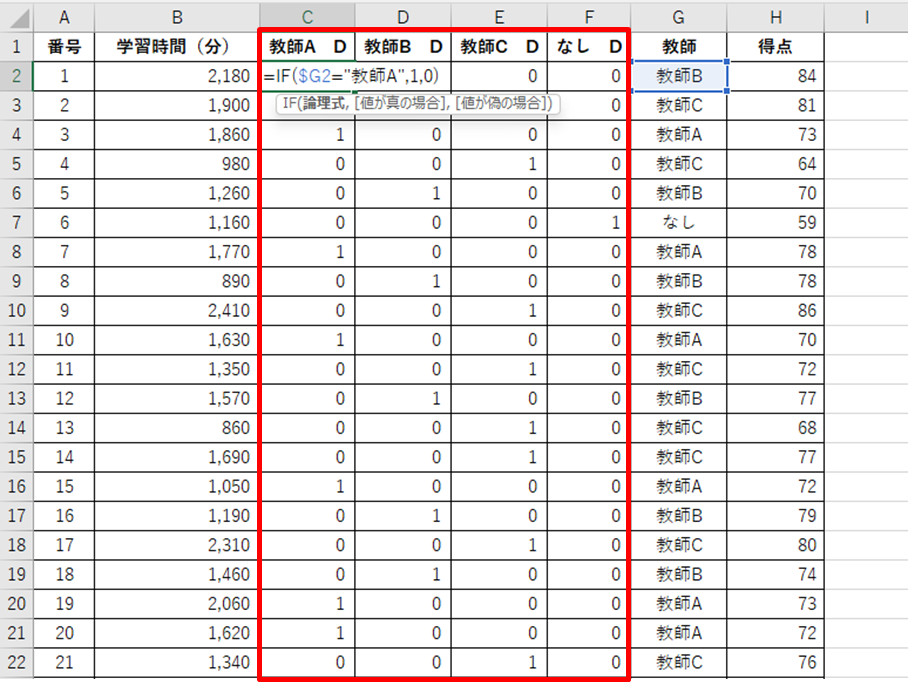
2.基準となるダミー変数を削除する(この場合「なし」とした)
3.残ったダミー変数と他の量的変数を用いて重回帰分析を行う
この方法により原因系変数の選択肢が3つ以上の場合でも回帰分析を行うことができます。
今回のまとめ
今回は「ビジネス統計スペシャリスト・エクセル分析スペシャリスト」の5章から10章までのExcelを使った統計問題をまとめました。試験問題では半分程度がExcelでの実践問題ですが、慣れれば操作自体は難しくないので参考にしていただければ幸いです。
エクセルを使った統計において仮説検定を勉強したい方は以下がお勧めです。エクセルの「データ分析」アドインを使用するので難しい計算式などはでてきませんし、資格取得も可能です。平易な言葉が使われているので数学が苦手な人でも理解しやすい書籍です。
エクセルを使った統計について一から勉強したい方は以下がお勧めです。平均や中央値など統計で用いる基本的な項目を平易な言葉でわかりやすく説明してくれています。仮説検定を勉強する前に読んでおくとよい書籍です。
Excelを使った統計について一通り勉強したい方は以下がお勧めです。やや数学的な計算が入った説明がありますが最低限の数式で統計を使いこなせるようにしてくださっています。





コメント